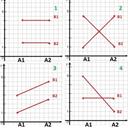
Bei der ANOVA wird die Varianz einer oder mehrerer Zielvariable(n) wird durch den Einfluss einer oder mehrerer Einflussvariablen (Faktoren) erklärt. Die einfachste Form der Varianzanalyse testet den Einfluss einer einzelnen nominalskalierten auf eine intervallskalierte Variable, indem sie die Mittelwerte der abhängigen Variable innerhalb der durch die Kategorien der unabhängigen Variable definierten Gruppen vergleicht.
https://de.wikipedia.org/wiki/Varianzanalyse
Was ist ANOVA / Varianzanalyse?
Als Varianzanalyse (ANOVA von englisch "analysis of variance") bezeichnet man eine große Gruppe datenanalytischer und strukturprüfender statistischer Verfahren, die zahlreiche unterschiedliche Anwendungen zulassen. Ihnen gemeinsam ist, dass sie Varianzen und Prüfgrößen berechnen, um Aufschlüsse über die hinter den Daten steckenden Gesetzmäßigkeiten zu erlangen.
Die Varianz einer oder mehrerer Zielvariable(n) wird dabei durch den Einfluss einer oder mehrerer Einflussvariablen (Faktoren) erklärt. Die einfachste Form der Varianzanalyse testet den Einfluss einer einzelnen nominalskalierten auf eine intervallskalierte Variable, indem sie die Mittelwerte der abhängigen Variable innerhalb der durch die Kategorien der unabhängigen Variable definierten Gruppen vergleicht.
Somit stellt die Varianzanalyse in ihrer einfachsten Form eine Alternative zum t-Test dar, die für Vergleiche zwischen mehr als zwei Gruppen geeignet ist.
Grundbegriffe
Die abhängige Variable heißt Zielvariable: Das ist die metrische Zufallsvariable, deren Wert durch die kategorialen Variablen erklärt werden soll. Die abhängige Variable enthält Messwerte.
Die unabhängige Variable nennt man Einflussvariable oder Faktor: Das ist die kategoriale Variable (= Faktor), die die Gruppen vorgibt. Ihr Einfluss soll überprüft werden, sie ist nominalskaliert.
Die Kategorien eines Faktors heißen dann Faktorstufen. Achtung: Diese Bezeichnung ist nicht identisch mit jener bei der Faktorenanalyse.
Anzahl der Zielvariablen
Je nachdem, ob eine oder mehrere Zielvariablen vorliegen, unterscheidet man zwei Formen der Varianzanalyse:
Die univariate Varianzanalyse, nach der englischen Bezeichnung analysis of variance auch als ANOVA bezeichnet.
Die multivariate Varianzanalyse, nach der englischen Bezeichnung multivariate analysis of variance auch als MANOVA bezeichnet
Je nachdem, ob ein oder mehrere Faktoren vorliegen, unterscheidet man zwischen einfaktorieller (einfacher) und mehrfaktorieller (multipler) Varianzanalyse.
Weiterhin unterscheidet man noch nach der Anzahl der Untersuchungseinheiten sowie zwischen festen und zufälligen Effekten.
SPSS-Output
Meistens nutzt man zur Berechnung von Varianzanalysen Computerprogramme, wie R oder SPSS. Bei einer einfaktoriellen Varianzanalyse ohne Messwiederholung sieht das Ergebnis in SPSS z.B. so aus:

Quelle: https://upload.wikimedia.org/wikipedia/commons/9/90/Anova_ergebnis.png
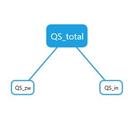
Um auf den F-Wert als statistischen Kennwert zu kommen, wurden die Quadratsummen (Sum of Squares) der verschiedenen Varianzquellen (Between, Within und Total) in Beziehung zu den Freiheitsgraden (df) gesetzt. In diesem Fall ist das Ergebnis signifikant!
Mehr dazu findest du in folgenden Lernsets: