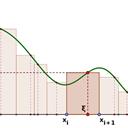
Eine Funktion ist eine eindeutige Abbildung von Werten einer Menge (Definitionsmenge) in eine andere Menge (Wertemenge). Funktionen ordnen allen x-Werten (den Werten der Definitionsmenge) genau einen y-Wert zu. Dabei bilden alle y-Werte zusammen die Wertemenge.
Ob es sich bei einer Zuordnung um eine Funktion handelt, ist leicht nachzuprüfen: wird jedem x-Wert genau ein y-Wert zugeordnet? Wenn das nicht der Fall ist, also beispielsweise einem x-Wert mehrere y-Werte zugeordnet werden, so handelt es sich nicht um eine Funktion.
Beispiel: Jedem Kind wird seine leibliche Mutter zugeordnet. (Funktion: Jedes Kind hat genau eine leibliche Mutter.)
Jeder Mutter wird ihr Kind zugeordnet. (Keine Funktion: Manche Mütter haben mehrere Kinder.)
Funktionen dienen der mathematischen Beschreibung von Vorgängen. Mit ihnen kann man Abhängigkeiten und Veränderungen erfassen und analysieren.
Funktionen können dargestellt werden durch eine Funktionsgleichung, eine Wertetabelle, einen Funktionsgraphen oder einen Beschreibungstext.
Es werden verschiedene Arten von Funktionen unterschieden. In der allgemeinen Schulmathematik sind diese relevant: Lineare Funktionen, Quadratische Funktionen, Trigonometrische Funktionen, Potenzfunktionen, Exponentialfunktionen und Gebrochenrationale Funktionen.
Wiki und Lernwerkzeug vereint!
