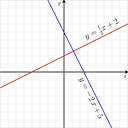
Lineare Funktionen erfüllen stets die Gleichung y = mx + n (m und n sind reelle Zahlen). Der Graph einer linearen Funktion ist stets eine Gerade. Im Bild zu sehen sind die graphischen Darstellungen der linearen Funktionen y = ½x +2 und y = -2x +5. Das Besondere hier ist, dass die beiden Geraden senkrecht aufeinander treffen - das liegt daran, dass die Anstiege der roten Funktion (m = ½) und der blauen Funktion (m = -2) zueinander negativ reziprok (-1:½ = -2) sind.
Lineare Funktionen erfüllen stets die Gleichung f(x) = mx + n. Statt f(x) kann auch y geschrieben werden (also y = mx + n). Dabei sind m und n reelle Zahlen. Lineare Funktionen sind also Polynomfunktionen höchstens ersten Grades: das x kommt nur in einfacher Potenz vor (kein x², x³, etc.).
Die reelle Zahl m beschreibt dabei den Anstieg, oder die Steigung der Geraden - also die Änderungsrate der Funktion. Änderungsrate bedeutet dabei: Wie ändert sich der y-Wert bei Änderung der x-Werte?
Die reelle Zahl n gibt an, an welcher Stelle die y-Achse von der Geraden geschnitten wird - sie wird daher auch y-Achsenabschnitt genannt. Der Schnittpunkt mit der y - Achse ist daher stets (0|n)
y - Achsenabschnitt n
Ist n = 0, also f(x) = mx so verläuft der Graph der Funktion f durch den Koordinatenursprung (0|0). Beispiel: Die Funktion y = 3x verläuft durch (0|0) - der Funktionswert (also y) des x-Wertes Null ist Null.
Ist n > 0, so schneidet der Graph der Funktion die y-Achse im positiven Bereich.
Ist n < 0, so schneidet der Graph der Funktion die y-Achse im negativen Bereich. Beispiel: Die Funktion y = 3x + 4 schneidet die y-Achse an der Stelle y = 4, der Schnittpunkt mit der y - Achse ist also (0|4). Die Funktion y = 3x -2 schneidet die y - Achse an der Stelle y = -2, der Schnittpunkt mit der y - Achse ist also (0|-2).
Steigung/Anstieg m
Ist m = 0, so verläuft der Graph der Funktion parallel zur x-Achse. *Beispiel: Der Graph der Funktion y = 3 schneidet die y-Achse im Punkt (0|3) und verläuft parallel zur x-Achse. Jedem x wird die Zahl 3 zugeordnet. *
Ist m < 0, so verläuft der Graph der Funktion monoton steigend (also schräg nach oben rechts).
Ist m < 0, so verläuft der Graph der Funktion monoton fallend (also schräg nach unten rechts).
Einzeichnen des Funktionsgraphen in ein Koordinatensystem
Finde m und n heraus.
Trage n auf der y-Achse ab. Du hast nun den Schnittpunkt (0|n) auf der y-Achse markiert.
Gehe von diesem Schnittpunkt mit der y-Achse (0|n) aus 1 Schritt nach rechts und m Schritte nach oben, wenn m > 0 und m Schritte nach unten, wenn m < 0. Markiere diesen Punkt. [Ist m ein Bruch (Zähler oberhalb des Bruchstrichs, Nenner unterhalb des Bruchstrichs), so gehst du die Nennerschritte nach rechts und dann die Zählerschritte nach oben (m > 0) oder nach unten (m < 0).]
Zeichne eine Gerade durch die beiden markierten Punkte.